Mandelbrot-Fraktal in Java

Mandelbrot-Fraktal in Java

Als eine Jahresarbeit am Schülerrechenzentrum Dresden ist ein Programm entstanden, welches der Berechnung des Mandelbrot-Fraktals.

Das Mandelbrot-Fraktal oder die Mandelbrot-Menge, da es hier eigentlich um die Menge an Zahlen geht, die eine bestimmte Bedingung erfüllen ist auf der komplexen Zahlenebene zu finden. Diese Zahlen sind durch zwei Einheiten dargestellt. Jede Komplexe Zahl C hat einen reellen Teil und einen imaginären Teil. Der imaginäre Teil hat die Eigenschaft mit der imaginären Einheit i kombiniert zu werden. . Somit sieht eine komplexe Zahl folgend aus:  . Vorstellen kann man sich die komplexen Zahlen auf zwei Zahlenstrahlen, die wie in einem Koordinatensystem zueinander stehen. Die x-Achse in einem Koordinatensystem bildet die reellen Zahlen ab und die y-Achse die imaginären. Weiterhin ist wichtig zu wissen, dass eine komplexe Zahl einen Betrag hat. Dieser Betrag entspricht dem Abstand zwischen dem Ursprung der Zahlenebene und unserer komplexe Zahl. Dementsprechend kann dieser mit Hilfe des Satz von Pythagoras berechnet werden. Doch wie entsteht jetzt in dieser Ebene so ein spannendes und fast unendliches Bild?

Dafür nimmt man sich eine komplexe Zahl in der neunen Zahlenebene. Nun wird ermittelt ob diese Zahl zur Mandelbrot-Menge gehört oder eben nicht. Dafür für geschaut ob die Zahl innerhalb einer bestimmen Iterationsvorschrift beschränkt ist.

Das z ist die Zahl über welche iteriert wird. Das c ist die Zahl, welche wir vorher ausgewählt habe. Später wird jedem Pixel in dem Bild eine solche komplexe Zahl zugeordnet. Nun können zwei Fälle auftreten. Entweder die Zahl oder vielmehr der Betrag der Zahl divergiert ins unendliche oder dieser ist beschränkt (konvergiert, bzw. bleibt in einem festgelegten Rahmen). Wenn die komplexe Zahl in diesem bestimmten Rahmen bleibt dann gehört diese zur Mandelbrot-Menge.

Das Bild entsteht nun im einfachsten Fall dadurch, dass wir jedem Pixel, dessen Zahl divergiert weiß einfärben und jeden Pixel, dessen Zahl konvergiert schwarz.

Wie sieht das ganze jetzt im Code aus? Um mit dem Computer mit komplexen Zahlen zu rechnen können wir den reellen und imaginären Teil voreinander trennen. Dafür müssen wir für den reellen Teil und für den imaginären Teil eine eigene Iterationsvorschrift erstellen.

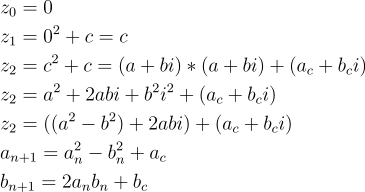
Erst wird angefangen mit den Variablen zu iterieren. Dann werden die komplexen Zahlen ausmultipliziert und eine neune komplexe Zahl. Diese addieren wird indem reeller Teil und imaginärer Teil getrennt addiert wird. Danach entstehen zwei neue Iterationsvorschriften.

Mit diesen Iterationsvorschriften können wir nun arbeiten und ein Programm schreiben um das Mandelbrot-Fraktal darzustellen. Um die Code recht einfach zu halten verwende ich Processing (Java).

void setup() {
  size(800, 800);
}

Hiermit erstellen wir ein neues Fenster mit dem Maßen von 800 mal 800 Pixeln.

void draw() {
  for (int x = 0; x < width; x++) {
    for (int y = 0; y < height; y++) {
      float a = map(x, 0, width, -2, 2);
      float b = map(y, 0, height, -2, 2);
    }
  }
}

Im Draw iterieren wir über jeden Pixel. Einmal x für die Breite und y für die Höhe. Mit der map()-Funktion rechnen wir die Pixel-Koordinaten in unsere Koordinaten für die komplexen Zahlen um. Pixel ganz links oben bekommen die Zahl (-2 + 2i) zugeordnet und Pixel ganz unten rechts (2 + 2i). Wie auch schon vorher ist a der reelle Teil und b der imaginäre.

void draw() {
  for (int x = 0; x < width; x++) {
    for (int y = 0; y < height; y++) {
      float a = map(x, 0, width, -2, 2);
      float b = map(y, 0, height, -2, 2);
      float ca = a;
      float cb = b;

      int n = 0;
      for(;n < 1000; n++) {

   
      }
    }
  }
}

Nun fügen wir eine Schleife hinzu, welche für uns die berechnet, ob der Zahl dazugehört oder nicht.

void draw() {
  for (int x = 0; x < width; x++) {
    for (int y = 0; y < height; y++) {
      float a = map(x, 0, width, -2, 2);
      float b = map(y, 0, height, -2, 2);
      float ca = a;
      float cb = b;

      int n = 0;
      for(;n < 1000; n++) {
        float newA = a*a - b*b;
        float newB = 2*a*b;
        a = newA + ca;
        b = newB + cb;
        if (sqrt(( a*a + b*b)) > 16) {
          break;
        }
      }
    }
  }
}

Nun fügen wie die Berchnung und eine weitere Abbruchbedingung hinzu. Sobald der Betrag über 16 kommt bestimmen wir die Zahl als divergierend.

void draw() {
  for (int x = 0; x < width; x++) {
    for (int y = 0; y < height; y++) {
      float a = map(x, 0, width, -2, 2);
      float b = map(y, 0, height, -2, 2);
      float ca = a;
      float cb = b;

      fill(0);
      int n = 0;
      for(;n < 1000; n++) {
        float newA = a*a - b*b;
        float newB = 2*a*b;
        a = newA + ca;
        b = newB + cb;
        if (sqrt(( a*a + b*b)) > 16) {
          fill(255);
          break;
        }
      }
      noStroke();
      rect(x, y, 1, 1);
    }
  }
}

Jetzt Fügen wir noch das Zeichnen der Menge hinzu. Wenn die Zahl divergiert, dann setzten wir die Farbe auf 255 (weiß) und überschreiben die vorher gesetzte Farbe 0 (schwarz). Wenn die Zahl währen der Iteration nicht divergiert dann bleibt die Farbe bei schwarz. Folglich zeichnen wir ein Viereck, welches 1×1 Pixel groß ist und auf den Pixelkoodinaten von vorher liegt. Hier das Ergebnis:

Download des Programms:

Mit Github zu einer weiteren tollen Darstellung: Multibrot