Facharbeit: Aufbau und Anwendung künstlich neuronaler Netzwerke
Diese Facharbeit ist als vorwissenschaftliche Arbeit in der 10. Klasse entstanden.
Inhaltsverzeichnis
- Einleitung
- Geschichte künstlich neuronaler Netzwerke
- Theorie hinter künstlichen Neuronen
- Topologie von künstlich neuronalen Netzwerken
- Lernverfahren von künstlich neuronalen Netzwerken
- Fazit und Schluss
- Literatur
1. Einleitung
Die heutige Zeit der Digitalisierung ist dadurch gekennzeichnet, dass der Mensch und Computer non-verbal und auch verbal miteinander kommunizieren können. Grundlage dafür sind künstlich neuronale Netzwerke, die für die Erstellung von künstlicher Intelligenz verwendet werden. Die Anwendung von künstlicher Intelligenz ist keine Utopie mehr. Die bekanntesten Verwendungsbeispiele sind Mustererkennungen in unterschiedlichen Bereichen. Bei Smartphones haben sich die Anwendung von Fingerabdrucksensoren, Gesichts- und Spracherkennung implementiert. Z.B. mit Apple Siri beantwortet der Computer einem jede erdenkliche Frage oder Amazon Alexa übernimmt die alltägliche Steuerung des Hauses. Auch in der Industrie wird an der Verwendung von künstlicher Intelligenz geforscht. Somit kommt der Begriff „Industrie 4.0“ ins Spiel. Weiterhin wird das autonome Fahren in naher Zukunft Wirklichkeit werden, was ein hohes Maß an künstlicher Intelligenz voraussetzt. Dies alles ist nur durch die Anwendung künstlich neuronaler Netzwerke möglich, da sich diese an verschiedene Gegebenheiten anpassen und Eingabeinformationen verarbeiten können.
Das besondere Interesse an diesem Thema ergibt sich aus der Teilnahme an einem Sonderkurs über künstliche neuronale Netzwerke im Schülerrechenzentrum Dresden im Schuljahr 2017/18. Die Entwicklung von solchen Computerprogrammen bietet neue, bisher ungeahnte Möglichkeiten. Bisher waren Algorithmen immer statisch und konnten sich im Grundlegenden nicht verändern. Durch künstlich neuronale Netzwerke wird eine Dynamik in der Algorithmen-Struktur geschaffen, welche mit der der Natur verglichen werden kann. Die Geschichte der Entwicklung von künstlich neuronalen Netzen wird in dieser Facharbeit beschrieben, ebenso wie der Aufbau, die Funktionsweise und die Anwendung. Es werden Vor- und Nachteile von verschiedenen Netzwerkarchitekturen und deren Verfahren dargestellt. Anhand in der Facharbeit aufgeführten Fakten wir die Frage, wodurch und wie künstlich neuronale Netzwerke lernen, beantwortet. Ebenso werden folgende Thesen geklärt und anschließend bewertet: „Durch künstliche Neuronen kann ein eindeutiges Abbild eines biologischen Neurons geschaffen werden“ und „Künstlich neuronale Netzwerke werden den biologischen Vorlagen zukünftig überlegen sein“. Diese Thesen stützen sich auf den Vergleich von künstlichen und biologischen neuronalen Systemen. Daher dient die Beschreibung einer Nervenzelle in einem biologischen Gehirn als Vorbild zur Entwicklung eines künstlichen Neurons, weil künstlich neuronale Netzwerke auf Grundlage der Natur entwickelt wurden. Die Funktionsweise eines kompletten Netzwerks aus künstlichen Neuronen wird durch ein konkretes Beispiel eines neuronalen Netzwerkes in der Programmiersprache Java verdeutlicht. Dies ergänzt die Argumentation, ob künstlich neuronale Netzwerke dem biologischen Vorbild künftig überlegen sein könnten.
2. Geschichte künstlich neuronaler Netzwerke
Die Entwicklung von künstlich neuronalen Netzwerken begann zwischen 1942 und 1955. In dieser Zeit entwickelten Walter Pitts und Warren McCulloch das erste technische Neuron, welches als Grundlage aller Netzwerkgenerationen gilt. Durch D. Hebb wurde das McCulloch-Pitts-Neuron weiterentwickelt. Er setzte den Grundstein der Entwicklung verschiedener Lernkonzepte von künstlich neuronalen Netzwerken. Der erste funktionsfähige Neurocomputer, welcher für die Mustererkennung verwendet wurde, hieß Perzeptron. Dieser wurde von Frank Rosenblatt entwickelt. Durch die weitere Erforschung von Verwendungszwecken stieß man schnell an eine Grenze bezüglich der Lernfähigkeit. Somit ließ das Interesse an künstlich neuronalen Netzwerken nach. Erst 1985 wurde durch Paul Werbos das Backpropagation-Verfahren vorgestellt, welches durch dynamische Lernverfahren die festgestellten Grenzen des Perzeptrons überschreitet. Somit erlangten künstlich neuronale Netzwerke einen neuen weiter andauernden Aufschwung. Heute werden künstlich neuronale Netzwerke in verschiedenen Bereichen verwendet und somit anwendungsspezifisch optimiert.
3. Theorie hinter künstlichen Neuronen
Viele technische Lösungen, welche einen Platz im modernen Leben eines Menschen gefunden haben, wurden von Wissenschaftlern in der Natur abgeschaut. Diese Herangehensweise beschreibt die Bionik. Zusammengefasst sucht sich die Bionik Vorbilder aus der Natur, um eine mögliche Konzeptionsidee für eine technische Lösung zu bekommen. In der Natur und auch in der Informatik ist das Neuron das grundlegende Element eines neuronalen Netzwerkes. Jedoch gibt die Natur aufgrund der zum Teil noch unerforschten bzw. kaum nachbaubaren komplexen biologischen Strukturen innerhalb und außerhalb von Nervenzellen keine für die Informatik realisierbare Lösung vor. Nur durch die Veränderung des Konzepts der Natur ist das sog. McCulloch-Pitts-Neuron entwickelt worden.
3. 1 Biologisches Neuron
Allgemein hat ein Neuron die Aufgabe, Erregungen zu empfangen und diese schließlich weiterzugeben. Dieses Konzept realisiert den Kontakt eines Lebewesens mit der Umgebung, jedoch auch die Informationsübermittlung innerhalb und zwischen Lebewesen. Beim Menschen, wie auch bei vielen anderen höherentwickelten Lebensformen, befinden sich Neuronen in Sinnesorganen, im Rückenmark und vor allem im Gehirn. Das Soma (Zellkörper) eines Neurons eines Menschen ist ungefähr fünf bis 100 Mikrometer groß, jedoch können die Ausläufer eines Neurons länger als ein Meter werden. Diese Größe wird für die Informationsübermittlung in einem Lebewesen z.B. im Rückenmark verwendet.
Ein biologisches Neuron besteht aus drei Teilen. Die Dendriten sind baumartige Ausläufer der Nervenzelle. Sie nehmen Erregungen von anderen Neuronen auf. Eine Erregung ist in diesem Fall ein elektrischer Impuls und wird als ein Reiz definiert. Ein Neuron kann mit einem elektrischen Kondensator verglichen werden. Der elektrische Speicher wird durch ein eingehendes Signal aufgeladen, bis ein bestimmter Schwellwert überschritten ist. Dann „feuert“ ein Neuron durch sein Axon das nächste Signal. Das Axon ist die Verbindungstrecke zwischen den nächsten Neuronen. Im Axon teilt sich das Signal und gelangt zu den Synapsen, welche die direkte Verbindung zwischen dem Axon und dem Dendriten des nächsten Neurons bildet. Bei den Synapsen, werden jedoch nicht zwei elektrische Leitungen direkt miteinander verbunden, sondern es gibt dazwischen einen kleinen Spalt. Die Verbindung über den Spalt wird von sog. Neurotransmitter realisiert. Dies sind chemische Substanzen, welche durch die elektrische Spannung ionisiert werden und somit das Signal
übermitteln. Die Leitfähigkeit der Neurotransmitter ist durch die Frequenz der Reize veränderbar und dadurch kann ein biologisches neuronales Netz lernen.
3. 2 Künstliches Neuron
Damit ein Neuron mit dem Vorbild aus der Natur für die Informatik brauchbar ist, muss es vereinfacht und in die mathematische Verarbeitung überführt werden. Deshalb spricht man in diesem Fall von einem Modell eines technischen Neurons. Dies verdeutlich, dass sich durch ein künstliches Neuron kein eindeutiges Abbild eines biologischen Gehirns erstellen lässt.
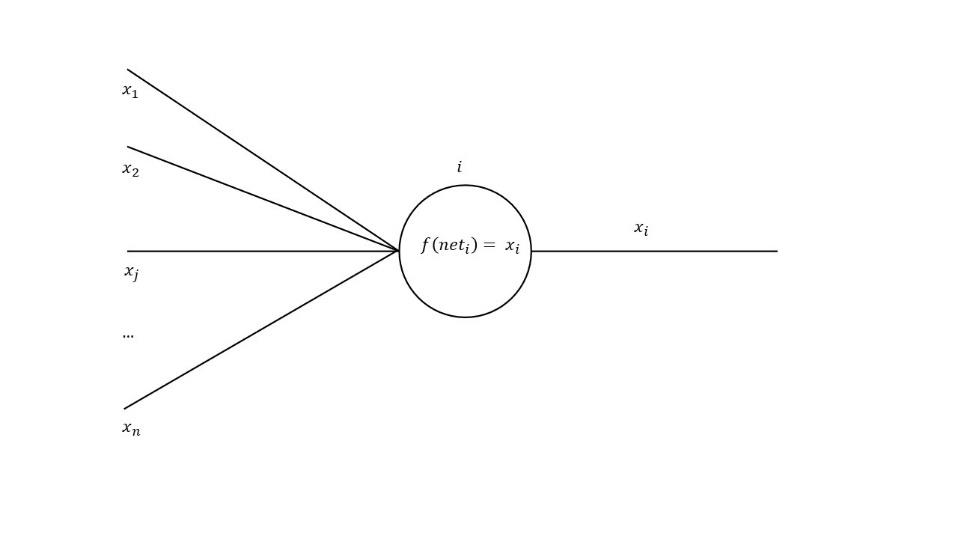
Die Dendriten (𝑥1,𝑥2,𝑥𝑗,…,𝑥𝑛) nehmen Signale von anderen Neuronen 𝑗 (𝑗∈ℕ) auf und leiten diese zum Körper des Neurons 𝑖 (𝑖∈ℕ). Die Weiterleitung der Signale geschieht durch die Eingabevektoren. Jeder Eingabevektor, auch Kante genannt, hat ein bestimmtes Gewicht. Dieses Gewicht (𝑤𝑖|𝑗) ist mit der Leitfähigkeit der Synapsen zu vergleichen. Es kann im positiven Bereich sein, dann hat diese Verbindung einen hohen Einfluss (exzitatorisch). Das Gewicht kann ebenso negativ sein, dann hat diese Verbindung einen hemmenden Einfluss (inhibitorisch). Keinen Einfluss hat das Neuron, wenn das Gewicht bei null liegt.4 Bei dem ursprünglichen McCulloch-Pitts-Neuron waren die Gewichte stetig fixiert. Jedoch änderte sich dies durch das Prinzip einer Lernregel von D. Hebb um 1949. Dabei wird das Gewicht jedes Neurons durch die Verwendung von Lernregeln verändert. Die Hebb‘sche-Lernregel wird in Punkt 5.1.2 näher erklärt.
Im Neuron wird nun die Ausgabe berechnet. Im ersten Schritt werden in der Propagierungsfunktion (𝑛𝑒𝑡𝑖=Σ𝑥𝑖𝑗 𝑤𝑖𝑗) die gewichteten Eingaben summiert. Diese Summe ist die Netzwerkeingabe oder auch der Netzwerkinput. Im nächsten Schritt wird mit der Aktivierungsfunktion (𝑓(𝑛𝑒𝑡𝑖)=𝑥𝑖) der Ausgabewert der Funktion ermittelt. Auf der Abszissenachse der Funktion ist die Eingabe (𝑛𝑒𝑡𝑖) und auf der Ordinatenachse wird die Aktivität oder auch die Ausgabe dargestellt. Für die Aktivierungsfunktion gibt es viele verschiedene Möglichkeiten. Zum einen kann eine
lineare Funktion (𝑓(𝑥)=𝑥) verwendet werden. Dabei ist die Eingabe der Ausgabe gleich. Diese Funktion ist jedoch nicht beschränkt und somit ist die Ausgabe fähig, unbegrenzt groß zu werden. Eine weitere Möglichkeit ist eine lineare Funktion mit Schwelle zu verwenden (Picewise-linear, engl. für teilweise Linear). Dies kann nützlich sein, wenn man in der Eingabe einen sehr niedrigen Netzwerkinput unterdrücken möchte. Doch auch diese Funktion kann einen unbegrenzt großen Ausgabewert erzeugen. Weiterhin kann man binäre Aktivierungsfunktion mit Schwelle (Θ) verwenden. Diese Funktion kann zwei Ausgaben haben. Diese Ausgaben können entweder über oder unter der Schwelle liegen.
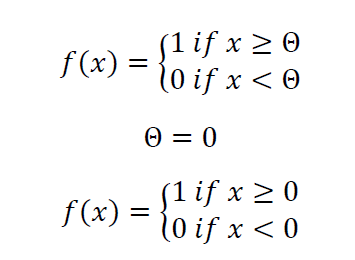
Die binäre Aktivierungsfunktion mit Schwelle kann ebenso als Stufenfunktion bezeichnet werden und wird für die Lösung binärer Probleme mit künstlich neuronalen Netzen verwendet. Normalerweise verwendet man eine logistische Funktion, da diese Funktion für die meisten Problemstellungen geeignet ist. Die am meisten gebräuchliche logistische Funktion als Aktivierungsfunktion ist die Sigmoidfunktion.
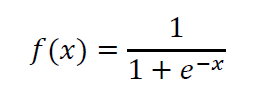
Das Grundprinzip des Lernens künstlich neuronaler Netze beruht damit auf Gewichten der Eingabevektoren, welche sich abhängig von der Ausgabe des Neurons verändern.
4. Topologie von künstlich neuronalen Netzwerken
4. 1 Verkettungsprinzipien
Die Erzeugung von künstlich neuronalen Netzte besteht darin, dass die Neuronen untereinander verknüpft werden. Dies geschieht nicht wie im menschlichen Gehirn, wo allein ein einzelnes Neuron mit knapp 1000 bis 10 000 anderen Neuronen in einer dreidimensionalen Struktur verbunden ist. In einem künstlichen neuronalen Netz wird diese Struktur vereinfacht. Es werden Schichten (engl. Layer) verwendet, in welche man die Neuronen einordnet. Wenn ein künstlich neuronales Netzwerk aus verschiedenen Schichten besteht, wird von einem Perzeptron-Netzwerk gesprochen. Alle Neuronen einer Schicht sind mit den Neuronen der nächsten Schicht verbunden. Somit spricht man von einer vollständigen Verknüpfung in eine Richtung, da die Informationen von Schicht zu Schicht nur in eine Richtung weitergegeben werden.
4.1.1 Einschichtiges vorwärts verkettetes Netzwerk
Ein einschichtig vorwärts verkettetes Netzwerk ist die einfachste Möglichkeit ein neuronales Netzwerk aufzubauen. Dabei besitzen Neuronen in den Input-Layern nur ein Eingang und ebenfalls nur einen Ausgang. Die Ausgabe der Input-Units ist die der ungewichteten Eingaben durch eine lineare Aktivierungsfunktion (𝑓(𝑥)=𝑥). In der nächsten Schicht sind Output-Units, welche die Eingaben mit der oben beschriebenen Funktionsweise verarbeiten und schließlich ein Ergebnis ausgeben. Ein Beispiel für ein solches Netz ist das sog. Deltanetwork, welches in dieser Arbeit implementiert wird.
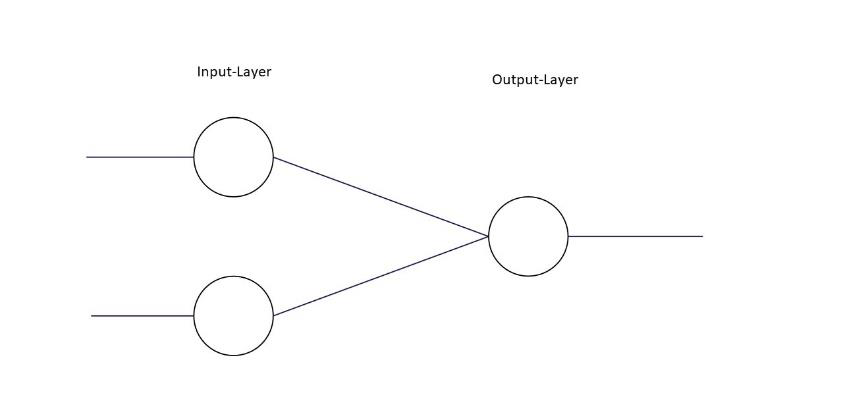
Dieses neuronale Netzwerk wird verwendet, um logische Operatoren wie AND (und), OR (oder), NOR (negiertes oder), NAND (negiertes und) zu lösen. Dabei nehmen die beiden Input-Units Reize auf, welcher ein Wahrheitswert (Boolean) ist (1 oder 0). Das Neuron im Output-Layer gibt ebenso ein Boolean aus, wobei dieser von einer reellen Zahl zwischen 0 und 1 gerundet wurde.
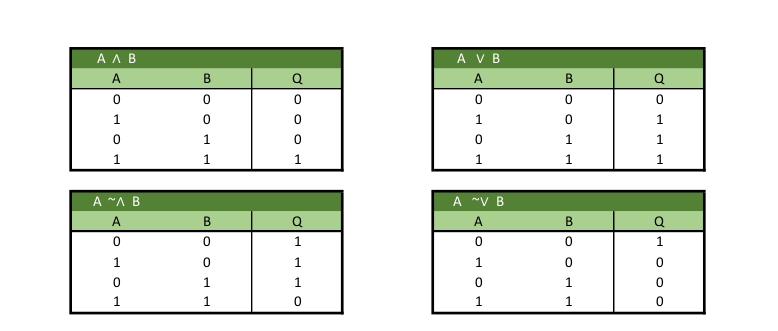
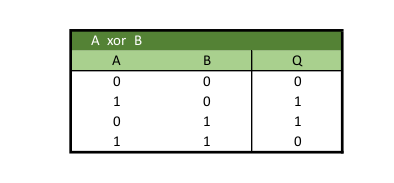
4.1.2 Mehrschichtiges vorwärts verkettetes Netzwerk
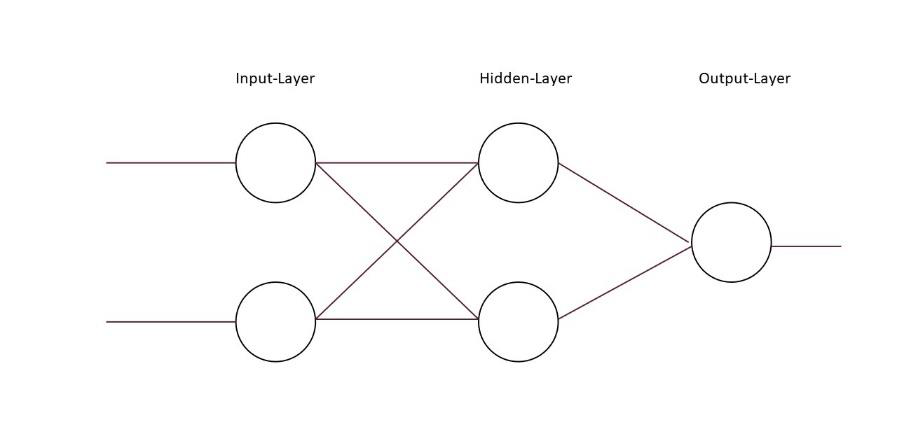
Mehrschichtige vorwärts verkettete Netzwerke entstehen dadurch, dass eine oder weitere Schichten hinzugefügt werden (Hidden-Layers). Durch das Hinzufügen der Hidden-Layers kann das neuronale Netzwerk komplexere Aufgaben lösen. Das bekannteste solcher neuronalen Netzwerke ist das ursprüngliche Perzeptron, wie in 4.2.2 beschrieben.
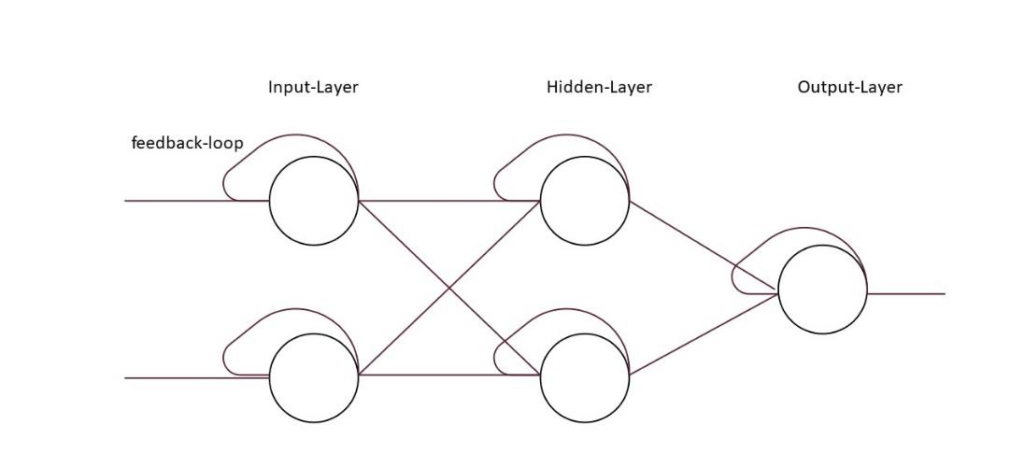
4.1.3 Rekurrentes Netzwerk
Ein rekurrentes Netzwerk ist bis auf ein entscheidendes Merkmal genau gleich aufgebaut wie andere neuronale Netzwerk. Die Ausgabe der Neuronen, wird durch eine sog. rekurrente Kante (engl. feedback loop) wieder an den Eingang des jeweiligen Neurons und an das Neuron in der nächsten Schicht weitergegeben. Dadurch ergibt sich der Grundsatz, dass eine Ausgabe, welche in der Vergangenheit geschehen ist, im nächsten Zeitintervall eine Eingabe sein wird. Der Vorteil dieser Netzwerke ist, dass ein Gedächtnis entsteht.
4.2 Das Perzeptron
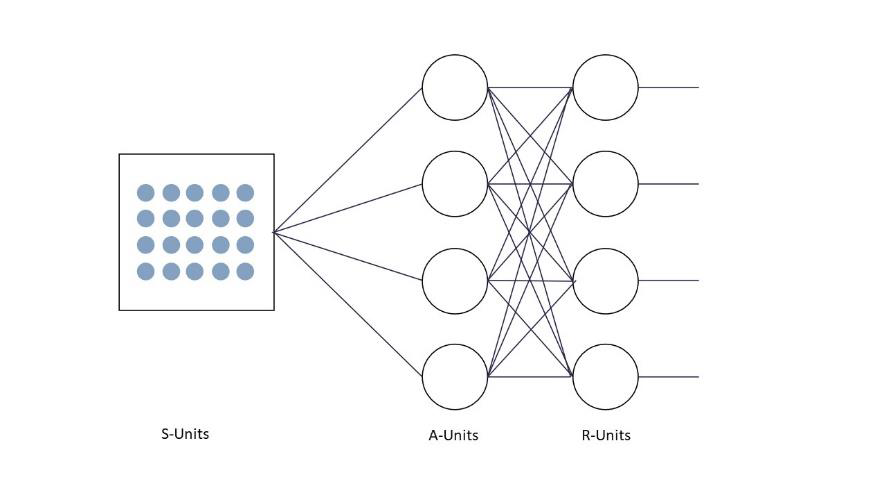
Das Perzeptron, wie in 2. verdeutlicht, stammt von einem amerikanischen Psychologen, welcher nach dem Vorbild des McCulloch-Pitts-Neurons ein erstes neuronales Netzwerk entwickelte. Das Perzeptron bestand aus einem Rasternetz von 400 Photozellen, welche den Input-Layer bilden. Diese Schicht bezeichnete er als S-Units oder auch Stimulationseinheiten, welche eine künstliche Netzhaut abbilden sollen. Die Photozellen der S-Unit werden nun zufällig mit Neuronen der Assoziationseinheiten (A-Units) verbunden. Auf dieser Verbindung sitzt ein unveränderbares Gewicht. Dadurch erhält jede Einheit der A-Units eine festgewichtige Eingabe. Die A-Units sind vollständig mit den R-Units verbunden. Das künstlich neuronale Netzwerk wurde verwendet, um Buchstaben zu erkennen. Jedoch war das Netzwerk eher unbrauchbar, da nur die Gewichte zwischen den Neuronen der A- und R-Units verändert werden können. Ebenfalls hatte das Netzwerk eine erhebliche mathematische Einschränkung. Das XOR-Problem, welches schon bei 4.2.1 erklärt wurde, blieb auch bei diesem Netzwerk ungelöst. Sobald das Perzeptron Muster erkennen sollte, welche nicht durch eine Gerade trennbar waren, versagte das Netzwerk.
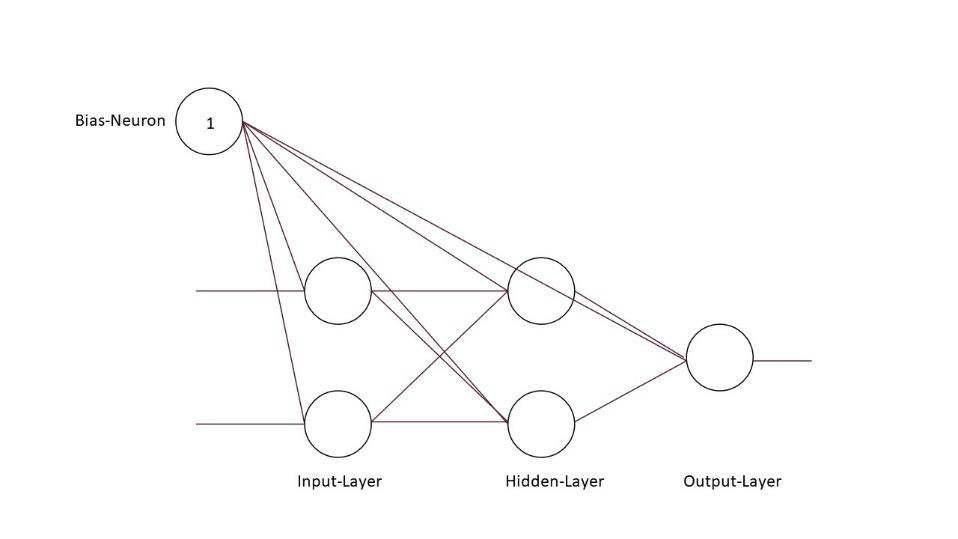
4.3 Bias-Neuron
Das Bias-Neuron oder die Bias-Unit, ist ein Neuron, welches keine Eingabe erhält und eine Aktivität von Eins hat. Die Bias-Unit ist mit jedem Neuron im Netzwerk verbunden. Zwischen den Bias-Neuron und den Neuronen, des Schichten, kann das Gewicht entweder positiv oder negativ sein. Durch diese Gegebenheiten wird bei jedem Neuron zu dem Netzwerkinput eine Aktivität von 1 multipliziert mit einem individuellen Gewicht addiert. Offensichtlich verzerrt das Bias-Neuron die Netzwerkeingabe und somit auch die Aktivität und Ausgabe der Neuronen (kognitive Verzerrung).
Die Funktion hinter der Bias-Unit, ist im Allgemeinen die Schwelle der Aktivierungsfunktion, wenn die Aktivierungsfunktion eine Sigmoidfunktion ist. Ein Vorteil, welcher sich dadurch ergibt ist, dass die Schwelle schneller veränderbar ist, da sich die Gewichte auch zwischen Bias-Neuron und den Neuronen der Schichten mit jedem Durchlauf verändern. Schließlich bedeutet das, dass die Bias-Unit die Neuronen zu einer Aktivität zwingt, wenn von den vorgelagerten Neuronen eine Eingabe gegeben null und das Gewicht zwischen Bias und dem Neuron der Schicht positiv ist. Auf der anderen Seite kann das Gewicht negativ sein, in diesem Fall wird sichergestellt, dass das Neuron auch bei einer hohen Eingabe erstmal bei einer niedrigen Ausgabe bleibt.
4.4 Vergleich der Struktur und Funktionsweise von künstlich neuronalen und biologisches Netzwerken
Durch die oben beschriebenen, in jedem Fall zweidimensionalen, Verkettungsprinzipien in Schichten wird ein künstlich neuronales Netzwerk eingeschränkt. Dies ist jedoch nur bedingt änderbar, da die bisherigen Algorithmen-Strukturen keine komplizierten Verkettungen zulassen. Jedoch sind neuronale Netzwerke unendlich über die oben beschriebenen Schichten erweiterbar. Über den Umfang an Schichten sind sie damit individuell an das zu lösende Problem adaptierbar. Ein biologisches Netzwerk muss für viele unterschiedliche Problemstellung funktionieren und muss somit universell sein. Diese Universalität wird durch die Dreidimensionalität gestützt, bei der jedes Neuron mit jedem indirekt und auch gleichzeitig interagieren kann.
Wenn ein Computer mit einem künstlich neuronalen Netzwerk arbeitet, geschieht dies durch die Verarbeitung und Weitergabe der Informationen in Zeitintervallen. Dies zeigt einen erheblichen Unterschied zu einem biologischen neuronalen Netzwerk, in dem die Neuronen nicht in vorgegebenen Zeitintervallen, sondern parallel zueinander agieren können. Die Tatsache, dass ein künstlich neuronales Netzwerk in Zeitintervallen arbeiten muss, verringert die universellen Möglichkeiten noch weiter. D.h. um die Leistungsfähigkeit eines biologischen Netzes mit seiner universellen Anwendbarkeit zu erreichen, würde ein künstlich neuronales Netz wesentlich längere Zeit benötigen. Es kann damit einem biologischen neuronalem Netzwerk nicht überlegen sein. Auf der anderen Seite kann ein künstlich neuronales Netzwerk ein biologisches bezüglich der Lernschnelligkeit für spezielle Problemstellungen, für die es konzipiert wurde, und bezüglich der Ausdauer übertreffen.
Der Nachteil der fehlenden Universalität von künstlichen Netzwerken kann durch Zusammenführung verschiedener, auf ein spezielles Problem zugeschnittener, künstlicher Netzwerke ausgeglichen werden, z.B. beim Bau von Humanoiden. Das könnte bedeuten, dass viele zusammengeschaltete künstliche Netzwerke die Leistungsfähigkeit biologischer Systeme übersteigen könnten. Aus meiner Sicht wird dies jedoch durch die eingeschränkte Kommunikation der künstlichen Netzwerke untereinander begrenzt. Am Beispiel des o.g. Humanoiden sind die Netzwerke für die Sinnesfunktion Sehen bzw. das Gleichgewicht und für Bewegung nicht so leistungsfähig miteinander gekoppelt wie im biologischen Vorbild. D.h. damit künstlich neuronale Netzwerke den biologischen Systemen gleichwertig oder überlegen sind, wären weitere Entwicklungen zur Kommunikation der künstlichen Netze untereinander oder zur Umsetzung von multidimensionalen Verkettungen notwendig.
Es gibt, wie oben für rekurrente Netzwerke beschrieben, bereits künstliche Systeme mit einem Gedächtnis. Dadurch, dass Ausgabeinformationen wieder als Eingabe fungieren, kann ein gewisses Gedächtnis erreicht werden. Dennoch ist durch das einfache Verkettungsprinzip und die Begrenzung in Schichten keine so umfassende „Erinnerung“ wie in einem biologischen neuronalen System möglich. Jedoch ist das Gedächtnis, d.h. die Speicherung von Daten in künstlichen Netzwerken, beständiger als die in biologischen Systemen. Das Gehirn ist darauf angewiesen, die Neuronen stetig zu nutzen, um Informationen abrufbereit zu halten.
5. Lernverfahren von künstlich neuronalen Netzwerken
5.1 Unterteilung
Die verschiedenen Lernverfahren der künstlich neuronalen Netzwerke werden verwendet, um einen passenden Algorithmus für ein Problem zu finden, welches durch ein künstlich neuronales Netzwerk gelöst werden. Im Allgemeinen wird in drei Formen des Lernens unterschieden. Diese Formen basieren auf ähnlichen Prinzipien wie bei dem biologischen Vorbild. Sie sind aber hinsichtlich der Umsetzung des Lernprozesses basierend auf mathematischen Methoden nicht mit den biochemischen bzw. biophysikalischen Prozessen im Nervensystem von Lebewesen vergleichbar.
5.1.1 Überwachtes Lernen (supervised learning)
Beim überwachten Lernen bestimmt ein Netzwerk aus den Eingaben in dem Input-Layer eine Ausgabe aus dem Output-Layer. Schließlich wird die Ausgabe des neuronalen Netzwerks mit einem vorgegebenen Lernziel verglichen. Es werden zwei verschiedene Lernregeln verwendet. Das Ziel der Lernregeln ist das Berechnen einer Gewichtsänderung zwischen zwei Neuronen. Im ersten Fall, der Delta-Lernregel, wird kein Hidden-Layer verwendet. Nachfolgend wird die Lernregel ausführlicher erläutert, weil das programmierte Beispielnetzwerk dieser Arbeit auf der Delta-Lernregel beruht.
Die Delta-Lernregel setzt die oben genannte Gesetzmäßigkeit mathematisch durch. Dabei wird ein Wert mit der Bezeichnung 𝛿 bestimmt. 𝛿 errechnet sich aus der Differenz der tatsächlichen Ausgabe und der Ausgabe des künstlich neuronalen Netzwerkes zu diesem Zeitpunkt 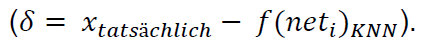
Durch diese Berechnung treten drei Fälle auf. Im ersten Fall liegt die Ausgabe des Netzwerkes unter der eigentlichen Ausgabe. In diesem Fall wird, wenn die Aktivität der Input-Units positiv ist, das Gewicht zu den Output-Units erhöht. Auf der anderen Seite wird das Gewicht verkleinert, wenn die Aktivität der Input-Units negativ ist. Der zweite Fall tritt ein, wenn die Aktivität des Netzes über dem eigentlichen Wert liegt. Wenn nun die Aktivität der Input-Units positiv ist, wird das Gewicht zu den Output-Units verkleinert und umgekehrt. Der letzte Fall ist das Optimum. Wenn die Ausgabe des Netzes gleich des eigentlichen Wertes ist, müssen keinerlei Verbesserungen vorgenommen werden.
Das künstlich neuronale Netzwerk hat eine bestimmte Aufgabe erlernt zu lösen. Daraus ergibt sich eine Formel für die Gewichtsänderung Δ𝑤𝑖𝑗:
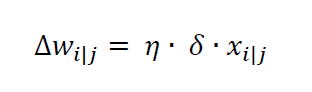
Die Lernrate 𝜂 beschreibt die Schritte in denen sich das Gewicht verändert und sich an das benötigte Gewicht „herantastet“. Die Lernrate ist ein Wert, welcher dem Netzwerk zu Beginn gegeben werden muss. Sie beeinflusst die Schnelligkeit des Lernens.
Nun kann das Netzwerk jedoch nicht nur zwei Schichten haben, sondern noch mindestens eine Weitere. In diesem Fall wird der sog. Backpropagation-Algorithmus verwendet, der folgendes Problem überwindet. Die Gewichtsänderung benötigt die Ausgabe des Neurons. Jedoch sind die Ausgabegrößen der Neuronen in den Hidden-Layern nicht gegeben. Daher kann ein solches Netzwerk vom Ende zurück propagieren (feedbackward). Vorab wird durch einen Vorwärtsdurchlauf (feedforward) vom Input- bis zum Output-Layer eine Ausgabe erzeugt und schließlich durch die Deltaregel ein Fehler 𝛿 definiert. Durch den nachfolgenden Rückwärtsdurchlauf (feedbackward) wird die Gewichtsänderung der einzelnen Neuronen bestimmt und somit die Gewichte angepasst. Dieser Zyklus wiederholt sich bis das Lernziel erreicht ist (𝛿=0).
5.1.2 Unüberwachtes Lernen (unsupervised-learning)
Beim unüberwachten Lernen eines neuronalen Netzwerkes wird dem Netzwerk nur ein Eingabemuster gegeben und anschließend verändert sich das neuronale Netzwerk seiner Ausgabe entsprechend. Dabei werden in der Eingabe Muster gesucht, welche schon einmal aufgetreten sind, um neue Informationen zu sortieren. Dies wird durch die Hebb‘sche Lernregel realisiert. Die Gewichtsänderung Δ𝑤𝑖|𝑗 ist das Produkt aus der Lernrate 𝜂, der Ausgabe des vorgelagerten und des nachgelagerten Neurons zwischen einer Kante.
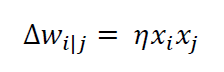
5.1.3 Bestärkendes Lernen (reinforcement learning)
Das bestärkende Lernen ist eine Kombination aus dem un- und überwachten Lernen. Hier wird dem neuronalen Netzwerk eine Eingabe gegeben und dieses erzeugt eine Ausgabe. Danach wird dem neuronalen Netzwerk mitgeteilt, ob die Ausgabe gut/richtig oder schlecht/falsch war. Dabei wird unter anderem durch einen reellen Wert noch angeben wie richtig oder falsch die Ausgabe war. Durch diese Gegebenheiten sucht sich das neuronale Netzwerk ein eigenes Ziel, welches bewertet wird.
5.2 Vergleich der Lernverfahren in biologischen und künstlichen Netzwerken
Die Lernverfahren von künstlich neuronalen Netzwerken haben mit der Biologie kaum etwas gemeinsam. Jedoch wurde ein grundlegendes Prinzip des Lernens von der Biologie adaptiert. In der Natur basiert das Lernen auf der unterschiedlichen Ausschüttung von Neurotransmittern, was mit den Gewichtsveränderungen der Lernregel vergleichbar ist. Ein großer Unterschied besteht auch noch darin sich Neuronen jederzeit mit anderen Neuronen neu verknüpfen, was die Verlinkung von verschiedenen Eingaben ermöglicht. Z.B. kann die visuelle und die auditive Wahrnehmung verbunden werden, wie das Hören eines bellenden Hundes mit der Vorstellung eines Hundebildes. Bei künstlichen Netzen können sich technische Neuronen nicht neu verknüpfen, was die Lernmöglichkeiten einschränkt.
Bei einem künstlich neuronalen Netzwerk kann zu einem Zeitpunkt nur eines der oben beschriebenen Lernverfahren verwendet werden. Um die Leistungsfähigkeit zu erhöhen, können alle Lernverfahren, jedoch nur nacheinander, angewendet werden. Die Grundlage für ein künstlich neuronales Netzwerk schafft das überwachte Lernen als einfachste Form. Aus dieser Grundlage an Wissen kann nun im unüberwachten Lernmodus oder sogar im bestärkenden Lernverfahren erweitert gelernt werden, d.h. zwischen verschiedenen Merkmalen differenziert werden. Der wesentliche Vorteil der Lernverfahren eines biologischen Systems ist jedoch, dass alle Prinzipien gleichzeitig verwendet werden.
5.3 Programmbeispiel eines künstlich neuronalen Netzwerkes
Das künstliche Netzwerk, welches im Rahmen dieser Arbeit programmiert wurde (Deltanetzwerk), löst logische Operatoren wie AND oder OR. Solche Operatoren sind Grundlage eines jeden PCs mit elektronischer Datenverarbeitung. Durch Verwendung dieser Operatoren in einem neuronalen Netz sind z.B. elektronische Bauteile abbildbar. Am Programmbeispiel wurde eine mathematisch lineare Problemstellung gelöst, d.h. das neuronale Netz hat gelernt, eine Datenmenge durch eine lineare Funktion zu teilen. Anwendung könnte ein solches Netzwerk finden, um große Datenmengen auf Unterschiede zu prüfen. Das Netzwerk ist in der Lage, das dargestellte Problem innerhalb von wenigen Sekunden durch künstliches Lernen (supervised learning, siehe 5.1.1) zu lösen. Im Vergleich dazu würde ein menschliches Gehirn als hochentwickeltes biologisches Netzwerk wesentlich länger brauchen, die Daten zu analysieren und die Unterschiede zu finden. Das dargestellte Beispielprogramm verdeutlicht die in dieser Arbeit erläuterten Unterschiede in der Struktur und Funktion sowie im Lernverhalten von künstlichen neuronalen und biologischen Netzwerken. Die höhere Lerngeschwindigkeit des Programms erklärt sich dadurch, dass es nur für ein spezifisches Problem zugeschnitten ist. Das angewendete Lernverfahren mittels der Delta-Lernregel ist ausreichend effizient. Die Nachteile bezogen auf die fehlenden Verknüpfungsmöglichkeiten spielen aufgrund der wenig komplexen Problemstellung in diesem Beispiel keine Rolle.
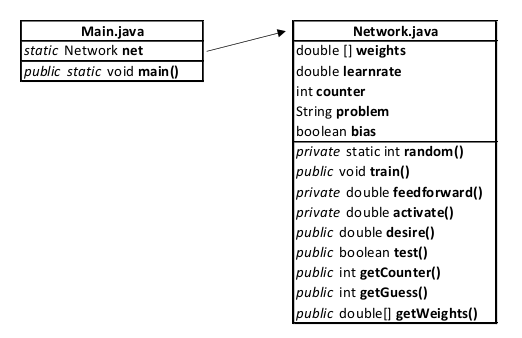
Das Programm für das Deltanetzwerk besteht aus zwei Klassen. Als Grundlage einer Klassenstruktur von Java steht die Hauptklasse „Main.java“. In dieser Klasse werden allgemeine Prozesse geregelt und der Ablauf festgelegt. Die zweite Klasse ist die „Network.java“, welche das künstlich neuronale Netzwerk abbilden soll und weiterhin alle Methoden für das Lernen enthält. Das numerisch indizierte Feld „weights“ umfasst alle Gewichte der Kanten. Die Variable „learnrate“ ist die Lernrate 𝜂. Der Integer „counter“ wird verwendet, um die Durchläufe zu zählen bis das neuronale Netzwerk das Problem vollständig erlernt hat und keine Veränderungen der Gewichte mehr benötigt. Die Zeichenkette „problem“ wird von der Main.java übergeben. Sie teilt dem Netzwerk mit, welches Problem gelöst werden soll. Weiterhin wird übergeben, ob das neuronale Netzwerk mit oder ohne Bias-Neuron arbeiten soll. Dies wird im Boolean „bias“ festgelegt. Damit das neuronale Netzwerk lernt, wird die Methode „train()“ aufgerufen. Nach der Ausführung der Methode kann mit der Methode „getGuess()“ eine individuelle Ausgabe erzeugt werden. Weitere öffentliche Methoden können genutzt werden, um netzinterne Variablen auszulesen. Die privaten Methoden werden für die Strukturierung des Lernprozesses verwendet.
//Main.java
package de.vincenteichhorn.main;
import java.util.Scanner;
public class Main {
static Network net;
public static void main(String[] args) {
String type = "or";
double learnrate = 0.01;
boolean bias = true;
net = new Network(type, learnrate, bias);
net.train();
Scanner s = new Scanner(System.in);
while (true) {
System.out.println(net.getCounter());
System.out.print("X:");
int x = s.nextInt();
System.out.print("Y:");
int y = s.nextInt();
System.out.println(x + " " + type + " " + y + " -> " + net.getGuess(x, y));
}
}
}#Network.java
package de.vincenteichhorn.main;
import java.util.Random;
public class Network {
double[] weights = new double[3];
double learnrate;
int counter;
String problem;
boolean bias;
public static int random(int min, int max) {
Random rand = new Random();
int randomNum = rand.nextInt((max - min) + 1) + min;
return randomNum;
}
Network(String prob, double c, boolean b) {
problem = prob;
learnrate = c;
bias = b;
weights[0] = random(-1, 1);
weights[1] = random(-1, 1);
weights[2] = random(-1, 1);
}
public void train() {
while(test() == false) {
int x = (int) random(0, 1);
int y = (int) random(0, 1);
double[] inputs = {x, y};
if(bias == true) {
inputs[inputs.length - 1] = 1;
}
double guess = feedforward(inputs);
double error = desire(inputs) - guess;
for (int i = 0; i < weights.length - 1; i++) {
weights[i] += learnrate * error * inputs[i];
}
counter++;
}
}
public double feedforward(double[] inputs) {
double neti = 0;
for (int i = 0; i < weights.length - 1; i++) {
neti += inputs[i] * weights[i];
}
return activate(neti);
}
private double activate(double x) {
if(x > 0.5) {
return 1;
} else {
return 0;
}
}
public double desire(double[] inputs) {
double x = inputs[0];
double y = inputs[1];
switch (problem) {
case "or":
if (x == 0 && y == 0) {
return 0;
} else {
return 1;
}
case "nand":
if (x == 1 && y == 1) {
return 0;
} else {
return 1;
}
case "nor":
if (x == 0 && y == 0) {
return 1;
} else {
return 0;
}
default:
if (x == 1 && y == 1) {
return 1;
} else {
return 0;
}
}
}
public boolean test() {
double[] data1 = {0,0};
double[] data2 = {0,1};
double[] data3 = {1,0};
double[] data4 = {1,1};
if(desire(data1) == feedforward(data1) &&
desire(data2) == feedforward(data2) &&
desire(data3) == feedforward(data3) &&
desire(data4) == feedforward(data4)) {
return true;
} else {
return false;
}
}
public int getCounter() {
return counter;
}
public int getGuess(int x, int y) {
double[] data = {x, y};
return (int) feedforward(data);
}
public double[] getWeights() {
return weights;
}
}
6. Fazit und Schluss
In der vorliegenden Facharbeit wurde beschrieben, wie künstlich neuronale Netze aufgebaut sind und wodurch diese lernen. Basierend auf den gleichen grundlegenden Prinzipien wie bei biologischen Netzen, der Veränderung von Signalen (bzw. Gewichten), existieren jedoch grundlegende Unterschiede in der Funktionsweise zwischen künstlichen neuronalen und biologischen Netzen. Im Wesentlichen bestehen diese darin, dass künstliche Systeme nur zweidimensional verkettet sind, in Zeitintervallen arbeiten sowie durch Organisation der technischen Neuronen in Schichten beschränkt werden. Damit ist die in der Einleitung aufgestellte These, dass durch künstliche Neuronen ein eindeutiges Abbild eines biologischen Neurons geschaffen werden kann, widerlegt. Künstlich neuronale Netze wurden auf Basis der biologischen Vorbilder entwickelt, sind aber aufgrund der anderen Struktur und Funktion nicht direkt mit diesen vergleichbar.
Die unterschiedliche Struktur und Funktionsweise beider Netzwerke mit den in der Arbeit beschriebenen Vor- und Nachteilen wirft die Frage auf, wie die zweite gestellte These „Künstlich neuronale Netzwerke werden den biologischen Vorlagen zukünftig überlegen sein“ zu bewerten ist. Meiner Ansicht nach, wird die Entscheidung, welche Netzwerk-Art, die künstlich -neuronale oder die biologische, die Überlegene ist, aufgrund der Lernfähigkeit fallen. Dies betrifft sowohl die Geschwindigkeit, als auch die Komplexität des Lernens. Das von mir programmierte Beispiel eines Deltanetzwerks für lineare Problemstellungen ist dem menschlichen Gehirn wegen seiner Geschwindigkeit zur Lösung eines spezifischen Problems überlegen. Für die Lösung komplexer Fragestellung bzw. Verknüpfung unterschiedlicher Probleme sind derartige künstlich neuronale Netze heutzutage den biologischen Systemen jedoch unterlegen. In der Zukunft werden künstliche Netze biologische Systeme potentiell übertreffen können, sofern die bisherigen Beschränkungen, wie fehlende Verknüpfung der Neuronen sowie die Nichtkommunikationen von Netzen untereinander, überwunden werden.
Die allgemeine Erkenntnis ist, dass nur durch eine Weiterentwicklung der Konzepte der künstlich neuronalen Netzwerke zwar kein eindeutiges, jedoch ein mindestens ebenbürtiges Abbild eines biologisch neuronalen Netzwerks entstehen kann. Die weitere Erforschung der biologischen Grundlagen dieser Thematik ist dafür essentiell, damit diese auf die Informatik übertragen werden können. Durch die Kombination der Vorteile der biologischen Funktionalitäten mit den Möglichkeiten der künstlichen Netzwerke könnten neuronalen Netzen mit verbesserten Eigenschaften entstehen. Diese würden eine maximierte Lerngeschwindigkeit und -ausdauer aufweisen, aber auch einen komplexen und universellen Einsatz ermöglichen.
7. Literatur
Monographien
- Callan, Robert (2003): Neuronale Netze im Klartext. München: Person Education Deutschland GmbH: Person Studium
- Ertel, Wolfgang (2008): Grundkurs Künstliche Intelligenz. Eine praxisortientierte Einführung. 1. Auflage. Wiesbaden: Friedr. Vieweg & Sohn Verlag | GWV Fachverlage GmbH.
- Fritzke, Bernd (1998): Vektorbasierte Neuronale Netze. Berichte aus der Informatik. 1. Auflage. Aachen: Schaker Verlag.
- Mainzer, Klaus (2016): Künstliche Intelligenz – Wann übernehmen die Maschinen?. 1. Auflage. Berlin Heidelberg: Springer-Verlag.
- Martin, Robert C. (2009): Clean Code – Refactoring, Patterns, Testen und Techniken für sauberen Code. 1. Auflage. Berlin Heidelberg: mitp.
Internetartikel
- Chemgapedia.de: Lineare Trennbarkeit (Linear Separability). URL: http://www.chemgapedia.de/vsengine/vlu/vsc/de/ch/13/vlu/daten/neuronalenetze/neuronalenetze1.vlu/Page/vsc/de/ch/13/anc/daten/neuronalenetze/snn7_3.vscml.html Letzter Aufruf am 1.12.2018
- Kreisel, David (dkreisel.com): Ein kleiner Überblick über Neuronale Netze. URL: http://www.dkriesel.com/_media/science/neuronalenetze-de-zeta2-2col-dkrieselcom.pdf Letzter Aufruf am 02.1.2019
- Neuronalesnetz.de: Neuronale Netze. Eine Einführung. URL: http://www.neuronalesnetz.de/downloads/neuronalesnetz_de.pdf Letzter Aufruf am 22.11.2018
- Neuronation.de: Was sind Gehirnzellen. Aufbau von Gehirnzellen. URL: https://www.neuronation.de/gehirntraining/was-sind-gehirnzellen Letzter Aufruf am 30.10.2018
- The Coding Train (youtube.com): 10: Neural Networks – The Nature of Code. URL:https://www.youtube.com/playlist?list=PLRqwX-V7Uu6aCibgK1PTWWu9by6XFdCfh Letzter Aufruf am 02.02.2018